ماتریس همانی چیست؟

در دنیای ریاضی، هر مفهوم می‌تواند دریچه‌ای جدیدی از چالش‌ها و ایده‌ها باشد. یکی از ابزارهای اساسی در زمینه جبر خطی، ماتریس همانی است. این ماتریس نه‌تنها درک ما از فضاهای چندبعدی را عمیق‌تر می‌کند، بلکه نقش کلیدی در تجزیه‌وتحلیل سیستم‌های معادلات خطی، تبدیل‌ها و حتی الگوریتم‌های پیچیده علمی و مهندسی ایفا می‌نماید. ماتریس همانی می‌تواند بازتابی از ساختارهای ریاضی و هندسی مشابه باشد. در این مقاله، به بررسی ویژگی‌ها، کاربردها و اهمیت این ماتریس در ریاضیات و علم داده خواهیم پرداخت و نشان خواهیم داد که چگونه این مفهوم ساده می‌تواند به ابزاری قدرتمند در دست پژوهشگران و مهندسان تبدیل شود.

آموزش ریاضی برای تمامی پایه‌ها با بهترین هزینه

مقدمه‌ای بر ماتریس همانی

ماتریس همانی (Identity Matrix) یک ماتریس مربعی (n × n) است که دارای عناصر ۱ در قطر اصلی و عناصر 0 در سایر مکان‌ها می‌باشد.

اهمیت ماتریس همانی در ریاضیات

• کاربرد در تبدیل‌ها و محاسبات: در جبر خطی، زمانی که از تبدیل‌های خطی یا تجزیه ماتریس استفاده می‌شود، ماتریس همانی به‌عنوان مبنای استاندارد برای نمایش‌های خطی و معادلات عمل می‌کند.
• در سیستم‌های معادلات خطی: ماتریس همانی در حل سیستم‌های معادلات خطی و در شکل استاندارد این معادلات (Ax = b) بسیار کاربرد دارد. در حل این معادلات به‌دست‌آوردن ماتریس معکوس نیاز است که در آن ماتریس همانی به کار ‌رود.

کاربردهای ماتریس همانی

• شناسه در پایگاه‌داده‌ها و طراحی الگوریتم‌: در برخی از الگوریتم‌ها، مانند الگوریتم‌های جستجو و مرتب‌سازی از ماتریس همانی برای نشان‌دادن عدم تغییر در داده‌ها استفاده می‌شود. به‌طورکلی، ماتریس همانی یکی از مفاهیم بنیادی در جبر خطی و ریاضیات است و بسیاری از ویژگی‌ها و کاربردهای آن در مباحث پیشرفته‌تر نیز وجود دارد.

مطلب پیشنهادی: چرا ریاضی رو یاد نمیگیرم؟

خصوصیات ماتریس همانی

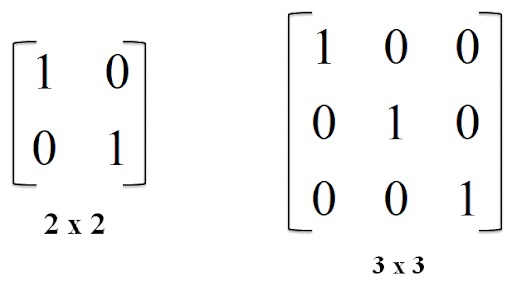
ماتریس همانی، یک ماتریس مربعی است که درایه‌های روی قطر اصلی آن برابر با ۱ و بقیه درایه‌ها برابر با ۰ هستند. به بیان دیگر:

• ماتریس همانی یک ماتریس n×n است، یعنی یک ماتریس مربعی است
• درایه‌های قطر اصلی این ماتریس همه برابر با ۱ هستند
• تمام درایه‌های خارج از قطر اصلی این ماتریس برابر با ۰ هستند

ماتریس همانی یکی از ابزارهای مهم در جبر خطی است و خواص خاصی دارد که در عملیات ضرب ماتریسی کاربرد پیدا می‌کند. ماتریس همانی یک ماتریس ویژه است که دارای خصوصیات منحصر به فردی نیز می‌باشد:

• تمام عناصر روی قطر اصلی آن برابر 1 هستند و سایر عناصر برابر 0 می‌باشند
• ضرب هر ماتریس m×n به نام A در ماتریس همانی به نتیجه‌ای برابر با خود ماتریس A می‌انجامد
• ماتریس همانی نقش عدد 1 را در محاسبات ماتریسی ایفا می‌کند، به همین دلیل گاهی به آن ماتریس یکانی نیز گفته می‌شود
• ماتریس همانی مانند عدد 1 عمل می‌کند و از ضرب هر ماتریس در آن، همان ماتریس به دست می‌آید
• اگر یک ماتریس با ماتریس همانی ضرب شود، نتیجه همان ماتریس اول خواهد بود

مطلب پیشنهادی: نحوه خواندن ریاضی برای کنکور

ویژگی‌های جبر خطی مرتبط با ماتریس همانی

ماتریس همانی دارای خصوصیات مهمی است که در جبر خطی کاربرد فراوانی دارد:

• هرگاه ماتریس A ضرب در ماتریس همانی انجام شود، حاصل همان ماتریس A خواهد بود
• ماتریس همانی نقش واحد ضرب را در جبر ماتریس‌ها ایفا می‌کند، همانند نقش عدد 1 در عملیات ضرب
• هر ماتریس مربعی با استفاده عملیات ابتدایی روی سطرها می‌تواند به ماتریس همانی تبدیل شود. این ویژگی در حل دستگاه معادلات خطی کاربرد دارد

بنابراین، ماتریس همانی به‌عنوان یک ماتریس خنثی در جبر خطی عمل می‌کند و درک خصوصیات آن برای درک بهتر ساختار و عملکرد ماتریس‌ها ضروری است.

کاربردهای ماتریس همانی در علوم مختلف

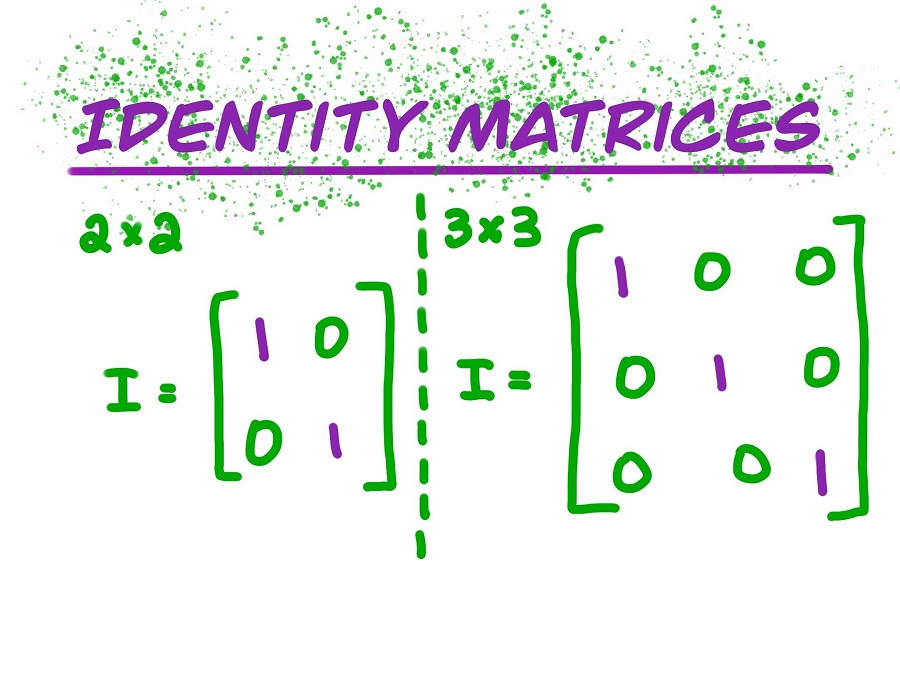
ماتریس همانی که به آن ماتریس واحد نیز گفته می‌شود، یک ماتریس مربعی است که تمام عناصر روی قطر اصلی آن برابر با یک و بقیه عناصر برابر با صفر است. کاربردهای ماتریس همانی در علوم مختلف شامل موارد زیر است:

ریاضیات

در حل معادلات خطی و سیستم‌های معادلات، ماتریس همانی به‌عنوان عنصر خنثی برای عمل ضرب ماتریسی استفاده می‌شود.

محاسبات عددی

در الگوریتم‌های عددی، از ماتریس همانی برای بازسازی و تعیین شرایط اولیه در حل معادلات استفاده می‌شود.

تحلیل داده‌ها و آمار

در تحلیل ماتریس مقادیر ویژه و ماتریس‌های کوواریانس، ماتریس همانی به‌عنوان مرجع برای محاسبات مقایسه‌ای به کار می‌رود.

گراف و شبکه‌ها

در نظریه گراف، ماتریس همانی می‌تواند به‌عنوان یک ابزار برای توضیح ویژگی‌ها و روابط میان رئوس یک گراف استفاده شود.

فیزیک

در آموزش فیزیک کوانتومی، ماتریس همانی حالت‌های مختلف را تحت‌تأثیر قرار نمی‌دهد.

برنامه‌نویسی و علوم کامپیوتر

در گرافیک کامپیوتری، ماتریس همانی برای انجام تبدیل‌های فضایی و نگه‌داشتن موقعیت‌های اصلی اشیاء استفاده می‌شود.

انتقال داده و رمزنگاری

در رمزنگاری، ماتریس همانی می‌تواند به‌عنوان بخشی از الگوریتم‌های رمزنگاری برای اطمینان از حفظ اطلاعات اورجینال استفاده شود.

مطلب پیشنهادی: چگونه موفق شویم؟

مثال‌های کاربردی از ماتریس همانی

در مجموع، ماتریس همانی یکی از ابزارهای اساسی در جبر خطی است که کاربردهای مهمی در محاسبات ماتریسی و حل معادلات خطی دارد:

1. تبدیل ماتریس به ماتریس واحد: ماتریس همانی به عنوان نقطه مبنا برای تبدیل یک ماتریس به ماتریس واحد (ماتریس مربعی که تمام درایه‌های قطر اصلی آن 1 و بقیه درایه‌ها 0 هستند) استفاده می‌شود. این عمل با انجام عملیات‌های سطری مقدماتی بر روی ماتریس همانی انجام می‌گیرد.
2. تعریف ماتریس وارون: ماتریس وارون یک ماتریس مربعی، ماتریسی است که حاصل ضرب آن با خود ماتریس مربعی، ماتریس همانی می‌شود. ماتریس همانی نقش مهمی در تعریف و محاسبه ماتریس وارون دارد.
3. بررسی وابستگی خطی: ماتریس همانی به عنوان یک ماتریس مرجع برای بررسی وابستگی خطی بردارهای ستونی یک ماتریس استفاده می‌شود.
4. محاسبه درجه یک ماتریس: درجه یک ماتریس برابر با رتبه آن است که با استفاده از ماتریس همانی قابل محاسبه است.
5. کاربرد در معادلات خطی: ماتریس همانی به عنوان یک ضریب واحد در معادلات خطی استفاده می‌شود که نشان دهنده انتقال بدون تغییر است.

رابطه ماتریس همانی با دیگر انواع ماتریس‌ها

رابطه این ماتریس با انواع دیگر ماتریس‌ها به‌صورت زیر است:

1. عملیات جمع و ضرب: وقتی ماتریس همانی را به یک ماتریس دیگر اضافه می‌کنیم، تأثیری بر آن نمی‌گذارد (در جمع به معنای ماتریس صفر است). اما اگر دو ماتریس را درهم ضرب کنیم و یکی از آن‌ها ماتریس همانی باشد، نتیجه برابر با ماتریس دیگری است.
2. ماتریس معکوس: برای هر ماتریس قابلیت معکوس (invertible) وجود دارد، اگر بتوانیم آن را با ماتریس همانی برابر کنیم. یعنی ضرب یک ماتریس معکوس با خود ماتریس، ماتریس همانی را تولید می‌کند.
3. ماتریس‌های مربعی: ماتریس همانی همیشه یک ماتریس مربعی است. این بدان معنی است که تعداد سطرها و ستون‌های آن برابر است و برای هر ابعادی می‌تواند وجود داشته باشد.
4. زیرمجموعه‌ای از ماتریس‌ها: ماتریس همانی یکی از انواع خاص ماتریس‌ها است و به طور خاص در نظریه ماتریس‌ها و جبر خطی اهمیت زیادی دارد.

مطلب پیشنهادی: نحوه خواندن ریاضی برای امتحان نهایی

ماتریس همانی و معکوس‌پذیری

ماتریس همانی ضرب ماتریسی را به هم نمی‌زند و هر ماتریس را در خود ضرب کند که در نتیجه همان ماتریس اصلی به دست می‌آید. بنابراین، معکوس پذیری ماتریس همانی به این معنی است که:

• ماتریس همانی دارای معکوس است، یعنی دیگر ماتریس‌هایی که در ضرب ماتریسی با ماتریس همانی ضرب شوند، به خود همان ماتریس باز می‌گردند
• معکوس ماتریس همانی، خود ماتریس همانی است. یعنی A^ (-1) = A
• پس می‌توان گفت که ماتریس همانی کاملاً معکوس‌پذیر است و معکوس آن همان خود ماتریس همانی است

چالش‌های مرتبط به حل مسئله ماتریس همانی

استفاده از ماتریس‌های همان می‌تواند با چالش‌ها و مسائل خاصی همراه باشد. در ادامه به برخی از این چالش‌ها اشاره شده است:

1. پیچیدگی محاسباتی: انجام محاسبات با ماتریس‌های بزرگ می‌تواند منجر به زمان‌های محاسباتی طولانی و مصرف بالای منابع شود. این موضوع به‌ویژه در برنامه‌های تعاملی یک چالش است.
2. خطاهای عددی: در محاسبات عددی با ماتریس‌ها، به‌ویژه در مقیاس‌های بزرگ یا در صورت وقوع مجموعه‌ای از تبدیل‌ها، خطاهای عددی ممکن است ایجاد شود. این خطاها می‌توانند نتایج نهایی را تحت تأثیر قرار دهند.
3. تبدیل‌های معکوس: در مواردی که به تبدیل معکوس (Inverse Transformation) نیاز داریم، محاسبه معکوس یک ماتریس می‌تواند مشکل‌ساز باشد، به‌ویژه اگر ماتریس دارای رتبه کامل نباشد یا معکوس آن به راحتی محاسبه نشود.
4. مدل‌سازی پیچیده: مدل‌های فیزیکی یا هندسی ممکن است نیاز به ترکیب روش‌های مختلف داشته باشند و درک و مدیریت این ترکیب ممکن است دشوار باشد.
5. تداخل با سیستم‌های دیگر: در یک سیستم پیچیده، ماتریس‌های همانی ممکن است با سایر ماتریس‌ها یا داده‌ها تداخل داشته باشند که می‌تواند به مشکلات هم‌زمانی و همپوشانی منجر شود.
6. انتقال داده‌ها: در برخی موارد، انتقال داده‌ها بین سیستم‌ها یا نرم‌افزارهای مختلف می‌تواند به مشکلات سازگاری انجامیده و نیازمند تبدیل‌های اضافی باشد.
7. رنگ و نورپردازی: در گرافیک کامپیوتری، استفاده از ماتریس‌های همانی در توصیف رنگ و نورپردازی می‌تواند پیچیدگی‌هایی ایجاد کند که نیاز به دانش عمیق در زمینه‌های فیزیکی و بصری دارد.

برای مواجهه با این چالش‌ها، پژوهشگران و مهندسان معمولاً از الگوریتم‌های بهینه، روش‌های عددی پایدار و تکنیک‌های کارآمد در زمینه‌های گرافیک و رباتیک بهره می‌برند.

سخن پایانی

ماتریس همانی یکی از مفاهیم بنیادی در جبر خطی و ریاضیات است. این ماتریس به‌عنوان یک نقطه عطف در عملیات ماتریسی شناخته می‌شود. ویژگی بارز ماتریس همانی این است که وقتی هر ماتریس دیگری با آن ضرب نتیجه همان ماتریس اولیه خواهد بود. ماتریس همانی علاوه بر ویژگی‌های جبری‌اش، در زمینه‌های مختلفی مانند سیستم‌های معادلات خطی، تجزیه‌وتحلیل داده‌ها، و بسیاری از کاربردهای مهندسی و علوم کامپیوتر اهمیت ویژه‌ای دارد.

سؤالات متداول

چگونه می‌توان از ماتریس همانی در حل معادلات استفاده کرد؟

در حل معادلات خطی، ماتریس همانی به‌عنوان معادل با عدد 1 در معادلات استفاده می‌شود و در یافتن معکوس ماتریس‌ها نقش مهمی دارد.

آیا می‌توان ماتریس همانی با ماتریس‌های دیگر جمع کرد؟

بله، ولی برای جمع کردن، باید ابعاد ماتریس‌ها برابر باشد.

چگونه می‌توان یک ماتریس همانی با ابعاد دلخواه ساخت؟

برای ساخت یک ماتریس همانی با ابعاد \(n\), می‌توان از بسته‌های برنامه‌نویسی مانند NumPy در پایتون استفاده کرد یا به‌سادگی یک ماتریس با عناصر 1 در قطر اصلی و 0 در سایر موارد نویسی کرد.