الگوریتم کروسکال چیست؟

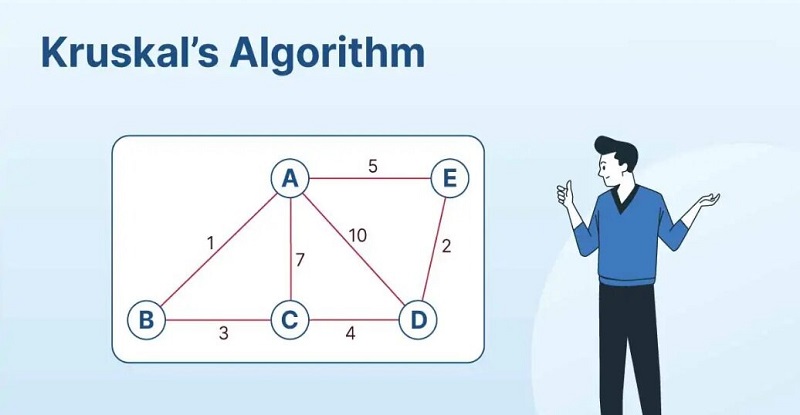
الگوریتم کروسکال یکی از روش‌های کارآمد برای حل مسئله درخت پوشای کمینه (Minimum Spanning Tree) در گراف‌ها می‌باشد. این طراحی الگوریتم که به نام ریچارد کروسکال، ریاضی‌دان و دانشمند آمریکایی نام‌گذاری شده، بر پایه ایده‌ای ساده و درعین‌حال مؤثر بنا گردیده است. در دنیای گراف‌ها، مسئله درخت پوشای کمینه از اهمیت ویژه‌ای برخوردار است؛ چراکه کاربردهای فراوانی در زمینه‌های مختلفی مانند شبکه‌های ارتباطی، طراحی مدارهای الکترونیکی و حتی مدیریت منابع انرژی دارد. الگوریتم کروسکال به دلیل سادگی و کارایی خود، یکی از گزینه‌های محبوب برای پیاده‌سازی در مسائل مرتبط با گراف‌ها است. اگر شما نیز در مورد نحوه عملکرد الگوریتم کروسکال پرسشی در ذهن دارید، حتماً این مقاله را تا به انتها دنبال نمایید.

تاریخچه و توسعه الگوریتم کروسکال

الگوریتم کروسکال یکی از مشهورترین الگوریتم‌ها برای حل مسئله حداقل درخت پوشای کمینه در گراف‌ها است. این الگوریتم به‌ویژه برای گراف‌های متصل و وزن‌دار کاربرد دارد و در بسیاری از زمینه‌های مختلف، از جمله شبکه‌های کامپیوتری و طراحی مدارها، استفاده می‌شود. مفهوم درخت پوشا و الگوریتم‌های مربوط به آن به نظریه گراف برمی‌گردد که در دهه‌های ۱۹۵۰ و ۱۹۶۰ توسعه یافت.

 آموزش هوش مصنوعی توسط مدرسین برتر کارآموز

مبانی الگوریتم کروسکال و کاربردهای آن

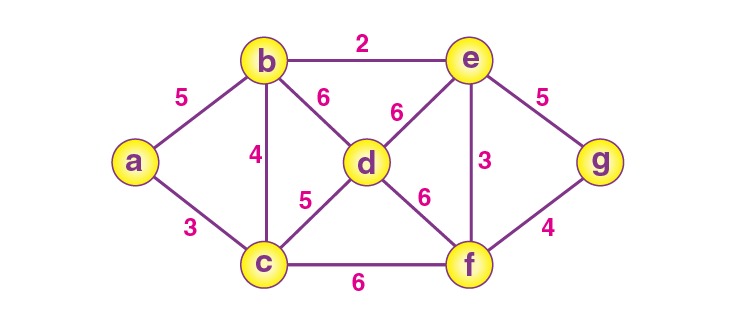
الگوریتم کروسکال شامل مراحل زیر است:

• همه یال‌های گراف را بر اساس وزن مرتب کنید.
• از یال‌های مرتب شده شروع کنید و هر یال را به درخت اضافه کنید.
• این کار را تا زمانی ادامه دهید که تعداد یال‌ها به تعداد رأس‌ها منهای یک برسد.

بهینه‌سازی الگوریتم از ساختار داده‌ای به نام ‌یافتن تجمعی (Union-Find) برای مدیریت و دنبال‌کردن مجموعه‌های متصل استفاده می‌کند. این ساختار داده کمک می‌نماید تا با کارایی بالاتری بتوانیم بررسی کنیم که آیا افزودن یک یال باعث ایجاد چرخه می‌شود یا خیر.

مطلب پیشنهادی: صف در ساختمان داده چیست؟

حوزه‌های استفاده از الگوریتم کروسکال:

1. شبکه‌های رایانه‌ای: برای طراحی شبکه‌هایی با کمترین هزینه برقراری اتصال
2. طراحی مدارهای الکترونیکی: بهینه‌سازی مسیرها برای کم‌کردن هزینه‌های مواد و اتصالات
3. حمل‌ونقل: برای دسترسی به بهترین مسیرها و کمترین هزینه‌های حمل‌ونقل

الگوریتم کروسکال به‌خاطر سادگی و کارایی‌اش یکی از ابزارهای کاربردی در نظریه گراف و عرصه‌های مختلف مهندسی و علوم کامپیوتر است.

اصول کارکرد الگوریتم کروسکال

الگوریتم کروسکال  یکی از الگوریتم‌های معروف برای پیداکردن اقلیدس شبکه  درخت پوشای کمینه در گراف‌های متصل غیر جهتی وزن‌دار است. این الگوریتم به‌گونه‌ای طراحی شده که با استفاده از مرتب‌سازی لبه‌ها و استفاده از ساختار داده‌ای به نام یونین ـ فایند، به حل مسئله بپردازد. در ادامه  اصول کارکرد این الگوریتم آورده شده است:

• مرتب‌سازی لبه‌ها:

تمامی لبه‌های گراف را بر حسب وزنشان به ترتیب صعودی مرتب کنید.

• ایجاد ساختار یونین ـ فایند:

یک ساختار داده‌ای به نام یونین ـ فایند  برای ردیابی مجموعه‌ها (گروه‌ها) ایجاد کنید. این ساختار کمک می‌کند تا تشخیص دهیم که آیا دو رأس در یک مجموعه قرار دارند یا خیر و همچنین بتوانیم دو مجموعه را با هم ادغام کنیم.

• انتخاب لبه‌ها:
  • از لبه‌های مرتب شده شروع کنید و به ترتیب آنها را بررسی کنید
  • اگر افزودن لبه‌ای به گراف به‌وجودآمدن حلقه منجر نشود (دو رأس این لبه در مجموعه‌های مختلف باشند)، آن لبه را به درخت پوشای کمینه اضافه کنید و دو مجموعه را ادغام کنید.
  • در غیر این صورت این لبه را نادیده بگیرید.
• تکرار:

مراحل 3 را ادامه دهید تا زمانی که تعداد لبه‌های درخت پوشای کمینه به تعداد راس‌ها منهای یک (|V| – 1) برسد.

• خروجی:

در نهایت، درخت پوشای کمینه (مجموع لبه‌ها) را خواهید داشت که وزن آن کمینه است.

الگوریتم کروسکال به دلیل سادگی در پیاده‌سازی و کارایی‌های مطلوب به‌خصوص برای گراف‌هایی با تعداد لبه‌های کمتر، به‌اشتراک‌گذاری در کاربردهایی مانند شبکه‌های رایانه‌ای، طراحی شبکه‌های توزیع انرژی و مسائل مشابه بسیار مورداستفاده قرار می‌گیرد.

مطلب پیشنهادی: پردازش داده چیست؟

مزایا و معایب الگوریتم کروسکال

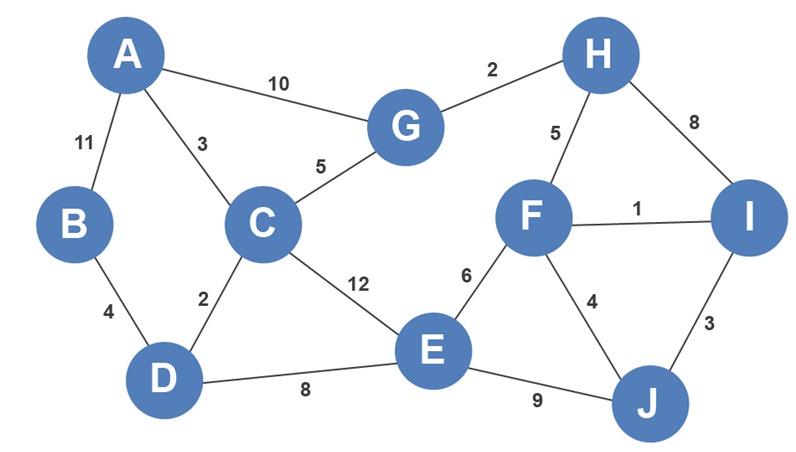
در ادامه به مزایا و معایب این الگوریتم اشاره شده است:

مزایا:

1. سادگی و وضوح: الگوریتم کروسکال دارای ساختاری ساده و قابل‌فهم است که به‌راحتی می‌توان آن را پیاده‌سازی کرد.
2. کارایی: این الگوریتم در گراف‌هایی که تعداد یال‌ها نسبت به تعداد رأس‌ها کم است، عملکرد بهتری دارد.
3. استفاده از ساختار داده‌های کارآمد: با استفاده از ساختار داده‌هایی مثل union-find، می‌توانیم زمان اجرای الگوریتم را به مقدار قابل‌توجهی کاهش دهیم.
4. یافتن درخت پوسته در گراف‌های غیر جهت‌دار: کروسکال به‌راحتی می‌تواند درخت پوسته را برای گراف‌های غیر جهت‌دار و وزن‌دار پیدا کند.

معایب:

1. نیاز به مرتب‌سازی: در ابتدا باید لیست یال‌ها را مرتب کرد که این فرآیند می‌تواند زمان‌بر باشد، به‌ویژه در گراف‌های بزرگی که تعداد یال‌ها زیاد است.
2. غیرقابل‌استفاده در گراف‌های جهت‌دار: این الگوریتم به طور خاص برای گراف‌های غیر جهت‌دار طراحی شده است و نمی‌تواند برای گراف‌های جهت‌دار استفاده شود.
3. پیچیدگی پیاده‌سازی در بعضی موارد: هرچند که الگوریتم ساده است، ولی پیاده‌سازی آن با استفاده از ساختار داده‌های پیشرفته ممکن است برای بعضی از برنامه‌نویس‌ها چالش‌برانگیز باشد.

مطلب پیشنهادی: الگوریتم علف هرز

کاربردهای الگوریتم کروسکال

الگوریتم کروسکال یکی از الگوریتم‌های معروف در نظریه گراف‌ها برای پیداکردن درخت پوشای کمینه در یک گراف ناهمپوش است. این الگوریتم کاربردهای متنوعی در دنیای واقعی دارد:

1. شبکه‌های ارتباطی: در طراحی شبکه‌های کامپیوتری، الگوریتم کروسکال می‌تواند برای تعیین کمینه هزینه‌های کابل‌کشی و اتصالات بین روترها استفاده شود.
2. طراحی شبکه‌های برق: برای اتصال ایستگاه‌های برق به یکدیگر و به مشتریان، به‌گونه‌ای که هزینه کل زیرساخت به حداقل برسد، از الگوریتم کروسکال استفاده می‌شود.
3. نقشه‌های جاده‌ای: در طراحی و برنامه‌ریزی جاده‌ها، این الگوریتم می‌تواند برای ایجاد یک شبکه جاده‌ای که تمامی نقاط را به هم متصل کند، به کار رود.
4. پروژه‌های زیرساختی: در پروژه‌های بزرگ مانند ساخت پل‌ها، تونل‌ها و سایر زیرساخت‌ها، می‌توان از الگوریتم کروسکال برای کاهش هزینه‌های ساخت و ایجاد اتصالات بهینه استفاده کرد.
5. تحلیل شبکه‌های اجتماعی: در تحلیل روابط بین افراد یا گروه‌ها، این الگوریتم می‌تواند به شناسایی ساختارهای کمینه و مهم‌تر در شبکه‌ها کمک کند.
6. مدیریت منابع: در سیستم‌های توزیع منابع مانند سیستم‌های آبرسانی یا توزیع گاز، می‌توان از الگوریتم کروسکال برای طراحی شبکه‌ای با کمترین هزینه و بالاترین کارایی استفاده کرد.

این مقاله را بخوانید: الگوریتم کلونی مورچگان

تفاوت‌های الگوریتم کروسکال با دیگر الگوریتم‌های مینیمم اسپنینگ (مانند الگوریتم پرایم)

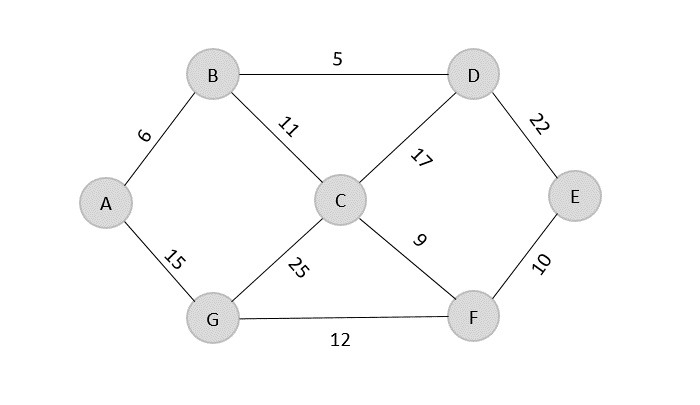
در ادامه به تفاوت‌های اصلی این دو الگوریتم اشاره می‌شود:

1. روش کار

الگوریتم کروسکال: این الگوریتم از روش “مرتب‌سازی و انتخاب” استفاده می‌کند. ابتدا تمام یال‌ها (لبه‌ها) گراف را بر اساس وزن‌هایشان مرتب می‌کند و سپس از کوچک‌ترین یال‌ها شروع به‌اضافه کردن به درخت می‌کند، به شرطی که این یال‌ها باعث ایجاد دور نشوند.

الگوریتم پرایم: این الگوریتم به طور تدریجی درخت پوشا را می‌سازد. در این روش، یک رأس را به‌عنوان نقطه شروع انتخاب می‌کنیم و در هر مرحله، یالی را که از  رأس‌های درخت پوشا به رأس‌های خارج از درخت متصل است و کمترین وزن را دارد، انتخاب می‌کنیم و به درخت اضافه می‌نماییم.

2. ساختار داده

کروسکال: این الگوریتم معمولاً به ساختار داده از نوع لیست یال‌ها و یافتن و اتحاد (Union-Find) نیاز دارد تا بررسی کند که آیا اضافه‌کردن یک یال باعث ایجاد دور می‌شود یا خیر.

پرایم: این الگوریتم معمولاً بر روی یک ساختار داده مبتنی بر لیست اولویت (Priority Queue) پیاده‌سازی می‌شود تا بتواند به‌آسانی یال‌های با کمترین وزن را پیدا کند.

3. پیچیدگی زمانی

کروسکال: پیچیدگی زمانی الگوریتم کروسکال به‌صورت (O(E log E)) است که (E) تعداد یال‌ها است. دلیل این زمان، نیاز به مرتب‌سازی یال‌ها و عملیات مجموعه‌ای است که ممکن است انجام شود.

پرایم: پیچیدگی زمانی الگوریتم پرایم بسته به استفاده از ساختار داده متفاوت است.

4. نوع گراف

کروسکال: این الگوریتم برای گراف‌های با یال‌های زیاد و زمانی که عدد یال‌ها بیشتر از تعداد رئوس است، مناسب است.

پرایم: این الگوریتم معمولاً برای گراف‌های با تعداد یال‌های کمتر عموماً مناسب‌تر است و برای گراف‌های متصل بسیار مناسب است.

5. قابلیت حل مشکلات خاص

کروسکال: مشکلش بیشتر مرتبط با بررسی دورها است و می‌تواند در برخی شرایط (مثل گراف‌های دوبخشی) کارآمدتر باشد.

پرایم: این الگوریتم می‌تواند به‌راحتی و به طور مؤثری در گراف‌های متصل با یال‌های با وزن کم تولید شده عمل نماید.

این مطلب را از دست ندهید: الگوریتم فیبوناچی چیست؟

مثال‌های عملی از استفاده از الگوریتم کروسکال

این الگوریتم به دلیل سادگی و کارایی‌اش در مسائل مختلف کاربرد دارد. در اینجا چند مثال عملی از کاربرد‌های الگوریتم کروسکال آورده شده است:

1. طراحی شبکه‌های ارتباطی

در طراحی شبکه‌های ارتباطی (مانند شبکه‌های تلفن، اینترنت، و…) هدف این است که هزینه نصب کابل‌ها و ارتباطات به حداقل برسد. با استفاده از الگوریتم کروسکال، می‌توان حداقل تعداد کابل‌های موردنیاز برای اتصال تمام نقاط (محل‌های داده، ایستگاه‌ها و…) را مشخص کرد.

2. طراحی شبکه‌های برق

در طراحی شبکه‌های توزیع برق، می‌توان از الگوریتم کروسکال برای اتصال ایستگاه‌های برق به یکدیگر با حداقل هزینه استفاده کرد. این امر می‌تواند به کاهش هزینه‌های ساخت و نگهداری شبکه کمک کند.

3. برنامه‌ریزی شهرسازی

در برنامه‌ریزی شهری، می‌توان از الگوریتم کروسکال برای طراحی شبکه‌ خیابان‌ها و مسیرهای حمل‌ونقل استفاده کرد. به‌این‌ترتیب، می‌توان مسیرهای اصلی را به‌صورت بهینه طراحی کرد تا ظرفیت و هزینه‌ها کاهش یابد.

4. مدیریت منابع

در مسائل مدیریت منابع، به‌ویژه در زمینه‌ کشاورزی و تولید انرژی، می‌توان از الگوریتم کروسکال برای بهینه‌سازی توزیع منابع میان مزرعه‌ها و مراکز تولید استفاده نمود.

5. تحلیل داده و بازیابی اطلاعات

در برخی الگوریتم‌های یادگیری ماشین و تحلیل داده، به‌خصوص در تحلیل خوشه‌بندی، می‌توان از الگوریتم کروسکال برای تشکیل خوشه‌ها و کاهش بعد داده‌ها استفاده کرد.

سخن پایانی

الگوریتم کروسکال به‌عنوان یکی از مؤثرترین روش‌ها برای پیداکردن درخت پوشای حداقل در گراف‌های وزن‌دار شناخته می‌شود. مزیت اصلی الگوریتم کروسکال، سادگی و کارایی آن در گراف‌های پراکنده و بزرگ است که آن را به ابزاری محبوب در علوم کامپیوتر و نظریه گراف تبدیل کرده است. با بهره‌گیری از این الگوریتم، می‌توان به طراحی شبکه‌های ارتباطی، بهینه‌سازی زیرساخت‌ها و حل مسائل مختلف در حوزه‌های مهندسی و علم داده پرداخت. در نهایت، درک عمیق‌تر از این الگوریتم و کاربردهای آن می‌تواند به ما کمک کند تا راه‌حل‌های بهتری برای چالش‌های پیچیده دنیای امروز ارائه دهیم.