آموزش زنجیره مارکوف در نرم افزار متلب

این روزها بیشتر مسائل در شاخه‌های مختلف، نیاز به تحلیل احتمالی دارند. در این راستا، زنجیره مارکوف مخصوصاً مونت کارلو در اکثر پروژه‌ها بسیار کاربردی عمل می‌کند. اما زنجیره مارکوف مونت کارلو چیست و چه انواعی دارد؟ برای پاسخ به این سوال با ما همراه باشید.

زنجیره مارکوف مونت کارلو (MCMC) چیست؟

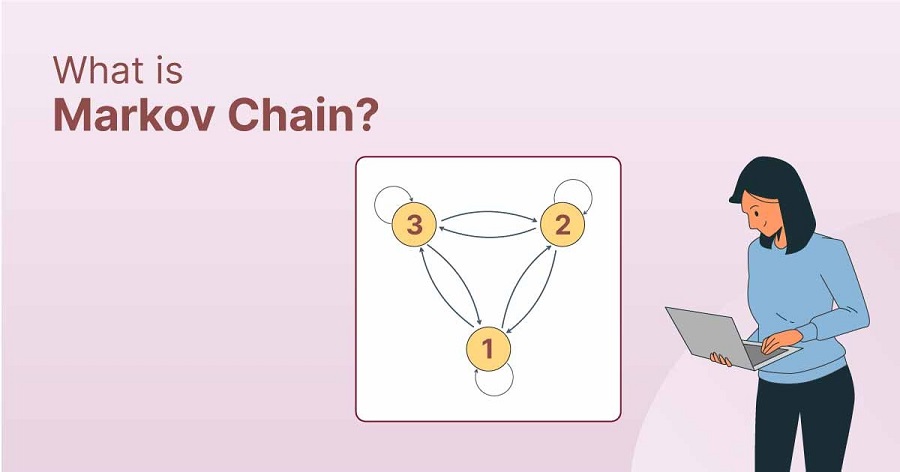
زنجیره مارکوف مونت کارلو، ابزاری قدرتمند برای نمونه برداری از توزیع‌های احتمالی پیچیده است و به افتخار ریاضی دان روس آندری مارکوف با این اسم شناخته می‌شود.
زنجیره مارکوف با نام الگوریتم مارکوف نیز شناخته می‌شود و یک سیستم ریاضیاتی است. زنجیره‌های مارکوف (Markov Chains) مدل‌های احتمالاتی هستند که در آن‌ها، وضعیت یک سیستم در زمان مورد بررسی به وضوح توسط وضعیت آن در زمان‌های گذشته تعیین می‌شود. در حالت ساده‌تر، زنجیره‌های مارکوف می‌توانند به عنوان یک سری زمانی از وضعیت‌ها باشند که هر وضعیت بر اساس وضعیت قبلی آن مشخص می‌شود. برای درک بهتر زنجیره مارکوف به مثال‌های زیر توجه کنید؛

• یک موجود زنده، فقط یک بار در روز غذا می‌خورد.
• اگر امروز هویج بخورد، فردا انگور یا پنیر را با احتمال برابر خواهد خورد.
• اگر امروز موز بخورد، فردا با احتمال 0.1 کاهو، احتمال 0.5 هویج و احتمال 0.4 پنیر می خورد.

با توجه به مثال‌های ذکر شده، عادات غذایی یک فرد را می‌توان به شکل زنجیره مارکوف در نظر گرفت. چرا که عادات غذایی که شخص برای روز بعد در نظر دارد، به امروزش کاملاً بستگی دارد.

آموزش متلب با بهترین هزینه

شبیه سازی مونت کارلو در متلب

شبیه سازی مونت کارلو در متلب یک روش قدرتمند برای حل مسائل پیچیده با استفاده از نمونه گیری تصادفی است. این روش به طور گسترده در زمینه های مختلف از جمله مهندسی، مالی و علوم فیزیک استفاده می شود.
در اینجا خلاصه ای از مراحل کلی شبیه سازی مونت کارلو در متلب ارائه شده است:

1. تعریف مساله:

ابتدا باید مساله‌ای را که می خواهید با استفاده از شبیه سازی مونت کارلو حل کنید، به طور دقیق تعریف کنید. این شامل تعریف تابع هدف، محدودیت ها و هر ورودی تصادفی مورد نیاز است.

2. نمونه گیری تصادفی:

از توابع تصادفی داخلی متلب برای تولید نمونه های تصادفی از فضای ورودی استفاده کنید. تعداد نمونه ها به دقت مورد نظر شما بستگی دارد.

3. محاسبه مقادیر تابع هدف:

برای هر نمونه تصادفی، مقدار تابع هدف را محاسبه کنید.

4. تخمین میانگین:

میانگین مقادیر تابع هدف را به عنوان تخمین میانگین واقعی تابع هدف محاسبه کنید.

5. تخمین واریانس:

واریانس مقادیر تابع هدف را به عنوان تخمین واریانس واقعی تابع هدف محاسبه کنید.

6. تجزیه و تحلیل نتایج:

نتایج را تجزیه و تحلیل کنید و در صورت نیاز شبیه سازی را با نمونه های بیشتر اجرا کنید.

در اینجا چند نمونه کد متلب برای انجام شبیه سازی‌های ساده مونت کارلو آورده شده است:

محاسبه عدد پی:

% تعداد نمونه ها

N = 100000;

% نقاط تصادفی در داخل دایره واحد

x = rand(N, 1);

y = rand(N, 1);

% نقاط داخل مربع

inside = (x.^2 + y.^2) <= 1;

% تخمین عدد پی

pi_estimate = 4 * sum(inside) / N;

% نمایش نتایج

fprintf(‘تخمین عدد پی: %f

‘, pi_estimate);

محاسبه انتگرال:

% تابع برای انتگرال

f = @(x) x.^2;

% حدود انتگرال

a = 0;

b = 1;

% تعداد نمونه ها

N = 100000;

% نقاط تصادفی در بازه انتگرال

x = a + (b – a) * rand(N, 1);

% تخمین انتگرال

integral_estimate = (b – a) * sum(f(x)) / N;

% نمایش نتایج

fprintf(‘تخمین انتگرال: %f

‘, integral_estimate);

اینها فقط نمونه‌های ساده‌ای هستند. شبیه سازی‌های مونت کارلو را می‌توان برای حل طیف گسترده ای از مسائل پیچیده‌تر در متلب استفاده کرد.

مطلب پیشنهادی: رگرسیون خطی چیست؟

انواع زنجیره مارکوف

زنجیره مارکوف دارای انواع مختلفی است که هر کدام ویژگی‌ها و مزایای خود را دارند. در ادامه به بررسی هر یک می‌پردازیم.

زنجیره مارکوف بر اساس زمان

• زنجیره مارکوف زمان گسسته: در این نوع زنجیره مارکوف، زمان به صورت مراحل مجزا در نظر گرفته می‌شود و احتمال وقوع هر حالت فقط به حالت قبلی بستگی دارد.
• زنجیره مارکوف پیوسته: در این نوع زنجیره مارکوف، زمان به صورت پیوسته در نظر گرفته می‌شود و احتمال وقوع هر حالت می‌تواند به کل تاریخچه‌ی قبلی زنجیره بستگی داشته باشد.

زنجیره مارکوف بر اساس حافظه

• زنجیره مارکوف بدون حافظه (مرتبه صفر): در این نوع زنجیره مارکوف، احتمال وقوع هر حالت فقط به حالت فعلی بستگی دارد و هیچ وابستگی به تاریخچه‌ی قبلی زنجیره وجود ندارد.
• زنجیره مارکوف با حافظه (مرتبه k): در این نوع زنجیره مارکوف، احتمال وقوع هر حالت به k حالت قبلی زنجیره بستگی دارد.

زنجیره مارکوف بر اساس فضای حالت

• زنجیره مارکوف گسسته: در این نوع زنجیره مارکوف، فضای حالت مجزا و محدود است.
• زنجیره مارکوف پیوسته: در این نوع زنجیره مارکوف، فضای حالت نامحدود است.