ماتریس چیست؟ تعریف ماتریس در ریاضی

ماتریس یک آرایه مستطیلی از اعداد، نمادها، نقاط یا کاراکترهایی است که هر کدام به یک سطر و ستون خاص تعلق دارند. یک ماتریس با ترتیب آن مشخص می‌شود که به شکل ردیف X و ستون Y  آورده شده است. اعداد، نمادها، نقاط یا کاراکترهای موجود در یک ماتریس را عناصر آن می‌نامند. مکان هر عنصر با سطر و ستونی که به آن تعلق دارد مشخص می‌شود.

ماتریس‌ها در ریاضیات اهمیت زیادی دارند. در این مقاله مقدماتی در مورد ماتریس‌ها، انواع و خواص آنها و موارد دیگر آشنا می‌شویم. اگر شما نیز پرسشی در ذهن خود دارید، حتماً تا به انتها این مقاله را دنبال کنید.

آموزش ریاضی در هر لحظه و هر جا با کارآموز

خواص ماتریس

یکی از ویژگی‌های مهم ماتریس‌ها اندازه آنها است که با تعداد سطرها و ستون‌ها تعریف می‌شود. ماتریسی با m  ردیف و n ستون به ماتریس mxn گفته می‌شود. اگر یک ماتریس دارای تعداد سطر و ستون یکسان باشد به آن ماتریس مربعی می‌گویند.

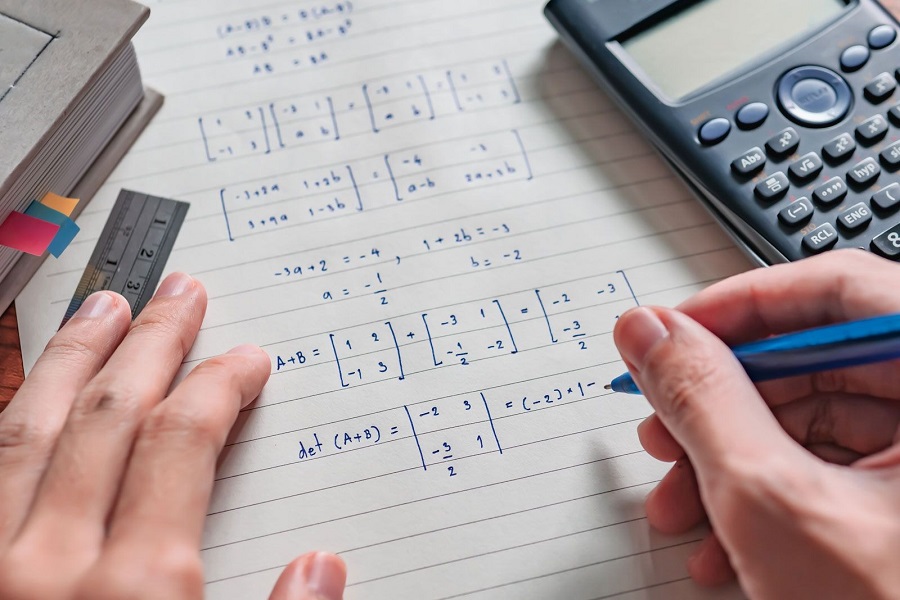
برای جمع یا تفریق دو ماتریس، عناصر موجود به‌سادگی جمع یا تفریق می‌شوند. حاصل‌ضرب دو ماتریس نیز یک ماتریس جدید است که عناصر آن مجموع حاصل‌ضرب عناصر در سطر و ستون مربوطه است.

در این مقاله، عملیات زیر در مورد ماتریس‌ها و خواص آنها را موردبحث قرار خواهیم داد:

• ماتریس اضافه
• تفریق ماتریس
• ضرب ماتریس‌ها

اضافه‌کردن ماتریس‌ها:

از جمع دو ماتریس Am*n و Bm*n ماتریس Cm*n به دست می‌آید. عناصر C مجموع عناصر متناظر در A و B هستند که می‌توان آنها را به‌صورت زیر نشان داد:

• جمع ماتریس‌ها قابلیت جا‌‌به‌جایی دارد؛ یعنی A+B = B+A
• جمع ماتریس‌ها بدین شکل است A+(B+C) = (A+B)+C
• ترتیب ماتریس‌های A، B و A+B همیشه یکسان است

تفریق ماتریس:

از تفریق دو ماتریس Am*n و Bm*n ماتریس Cm*n به دست می‌آید. عناصر C تفاوت عناصر متناظر در A و B هستند که می‌توانند به‌صورت زیر نمایش داده شوند:

• تفریق ماتریس‌ها غیر تعویضی است که به معنی A-B ≠ B-A است
• تفریق ماتریس‌ها بدین شکل است:A- (B-C) ≠ (A-B)-C
• ترتیب ماتریس‌های A، B و A – B همیشه یکسان است
• اگر ترتیب A و B متفاوت باشد، A – B قابل‌محاسبه نیست

ضرب ماتریس:

از ضرب دو ماتریس Am*n و Bn*p ماتریس Cm*p به دست می‌آید. این بدان معناست که تعدادی از ستون‌های A باید با تعداد ردیف‌های B برابر باشد تا C=A*B محاسبه شود. برای محاسبه عنصر c11، عناصر ردیف اول A را در ستون اول B ضرب کنید و آنها را جمع کنید.

• ضرب ماتریس‌ها غیر تعویضی است که به معنی A*B ≠ B*A است
• ضرب ماتریس‌ها بدین شکل است:A*(B*C) = (A*B)*C

برای محاسبه A*B، تعداد ستون‌های A باید با تعداد ردیف‌های B برابر باشد.

مطلب پیشنهادی: روش خواندن ریاضی برای امتحان نهایی

تبدیل ماتریس

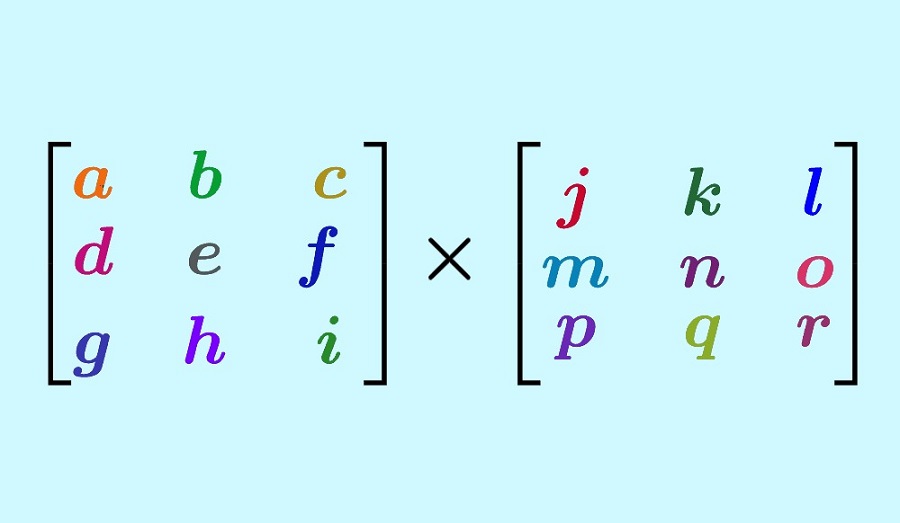
ماتریس‌ها را می‌توان از طریق عملیات های مختلفی مانند جابه‌جایی، وارونگی و مورب تبدیل کرد.

جا‌به‌جایی ماتریس

جابه‌جایی یک ماتریس یک ماتریس جدید است که با انعکاس ماتریس اصلی بر روی قطر اصلی آن تشکیل می‌شود. به‌عبارت‌دیگر، ردیف‌های ماتریس اصلی به ستون‌های ماتریس جابه‌جا شده تبدیل می‌شوند و بالعکس.

وارونگی ماتریس

وارونگی فرآیند یافتن ماتریسی است که وقتی در ماتریس اصلی ضرب شود، ماتریس هویت به دست می‌آید. به عبارت دیگر، اگر A یک ماتریس و A^(-1) معکوس آن باشد، A * A^(-1) = A^(-1) * A = I.  همه ماتریس ها معکوس ندارند، اما اگر a ماتریس معکوس دارد، منحصر به فرد است.

مورب سازی

قطری سازی فرآیند یافتن یک ماتریس مورب است که مشابه ماتریس اصلی است. این بدان معنی است که یک ماتریس معکوس P وجود دارد به‌طوری‌که P^ (-1) * A * P = D که در آن D یک ماتریس مورب است. مورب سازی می‌تواند مفید باشد؛ چون می‌تواند محاسبه مقادیر و بردارهای ویژه که نقش مهمی در بسیاری از زمینه‌های ریاضیات، علوم و مهندسی دارند، ساده کند.

یک مقدار ویژه ماتریس A یک اسکالر است به‌طوری‌که Av = v که در آن v یک بردار غیرصفر است که بردار ویژه نامیده می‌شود. بردارهای ویژه و مقادیر ویژه یک ماتریس را می‌توان برای مطالعه خواص تبدیل‌های خطی و حل سیستم‌های معادلات استفاده کرد.

همچنین از ماتریس‌ها برای نمایش تبدیل‌های خطی در جبر خطی استفاده می‌شود. تبدیل خطی تابعی است که بردارها را نگاشت می‌کند و خواص جمع بردار و ضرب اسکالر را حفظ می‌نماید. نمایش ماتریسی یک تبدیل خطی به ما این امکان را می‌دهد که تبدیل مؤثری انجام دهیم.

مطلب پیشنهادی: نحوه خواندن ریاضی برای کنکور

انواع ماتریس‌ها

بر اساس تعداد سطرها و ستون‌های موجود و ویژگی‌های خاص نشان‌داده‌شده، ماتریس‌ها به انواع مختلفی طبقه‌بندی می‌شوند:

• ماتریس سطری: ماتریسی که در آن فقط یک سطر وجود دارد و هیچ ستونی ندارد، ماتریس سطری نامیده می‌شود.
• ماتریس ستونی: ماتریسی که در آن فقط یک ستون وجود دارد و هیچ سطری وجود ندارد، ماتریس ستونی نامیده می‌شود.
• ماتریس افقی: ماتریسی که تعداد سطرهای آن کمتر از تعداد ستون‌ها باشد، ماتریس افقی نامیده می‌شود.
• ماتریس عمودی: ماتریسی که تعداد ستون‌های آن کمتر از تعداد سطرها باشد، ماتریس عمودی نامیده می‌شود.
• ماتریس مستطیلی: به ماتریسی که تعداد سطرها و ستون‌های آن نابرابر است، ماتریس مستطیلی می‌گویند.
• ماتریس مربع: به ماتریسی که تعداد سطرها و ستون‌های آن یکسان است، ماتریس مربع می‌گویند.
• ماتریس مورب: ماتریس مربعی که در آن عناصر غیرقطری صفر باشد، ماتریس مورب نامیده می‌شود.
• ماتریس صفر یا تهی: به ماتریسی که تمام عناصر آن صفر است، ماتریس صفر می‌گویند. ماتریس صفر را ماتریس تهی نیز می‌نامند.
• ماتریس واحد یا هویت: به ماتریس مورب که تمام عناصر مورب آن 1 است، ماتریس واحد می گویند. ماتریس واحد را ماتریس هویت نیز می نامند. یک ماتریس هویت با I نشان داده می شود.
• ماتریس متقارن: به ماتریس مربعی متقارن گفته می‌شود که جابه‌جایی ماتریس اصلی برابر با ماتریس اولیه باشد.
• ماتریس مثلثی بالایی: ماتریس مربعی که در آن تمام عناصر زیر مورب صفر هستند، به‌عنوان ماتریس مثلث بالایی شناخته می‌شود.
• ماتریس مثلث پایینی: ماتریس مربعی که در آن تمام عناصر بالای مورب صفر هستند، به‌عنوان ماتریس مثلث پایینی شناخته می‌شود.
• ماتریس مفرد: ماتریس مربعی به ماتریس مفرد گفته می‌شود که تعیین‌کننده آن صفر باشد.
• ماتریس غیر مفرد: ماتریس مربعی به ماتریس غیر مفرد گفته می‌شود که تعیین‌کننده آن غیرصفر باشد.

مطلب پیشنهادی: دلایل مهمی که ریاضی را یاد نمی‌گیریم

کاربرد ماتریس

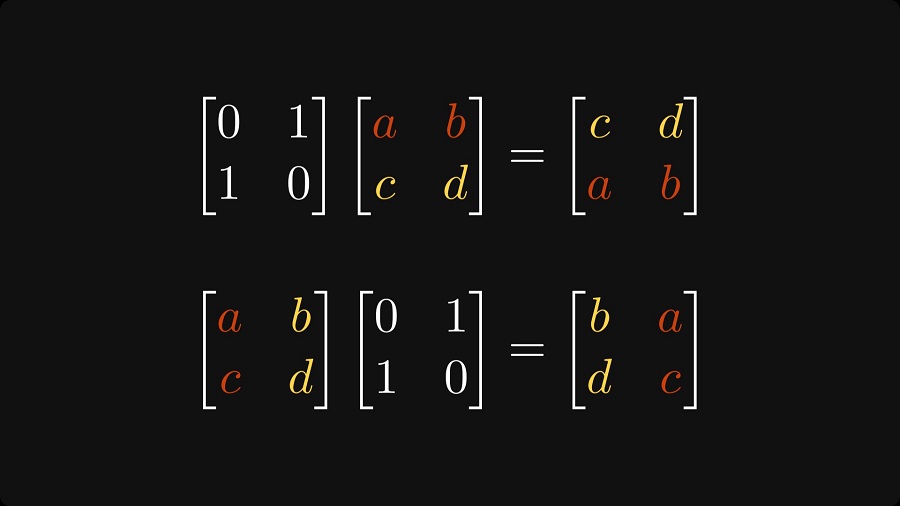
ماتریس‌ها کاربردهای زیادی در زمینه‌های مختلف دارند. در گرافیک کامپیوتری، ماتریس‌ها برای نمایش تبدیل‌هایی مانند چرخش، ترجمه و مقیاس‌بندی استفاده می‌شوند. در اقتصاد، ماتریس‌ها برای مدل‌سازی سیستم‌های معادلات خطی که روابط بین متغیرها، مانند عرضه و تقاضا را نشان می‌دهند، کاربرد دارد. در فیزیک، ماتریس‌ها برای نمایش کمیت‌های فیزیکی، مانند موقعیت و تکانه، و برای توصیف تکامل سیستم‌های فیزیکی در طول زمان مفید هستند.

در آمار، از ماتریس‌ها برای نمایش مجموعه‌داده‌ها استفاده می‌شود، جایی که هر ردیف نشان‌دهنده یک مشاهده و هر ستون به معنی یک متغیر است. تکنیک‌های تجزیه‌وتحلیل مؤلفه‌های اصلی و تجزیه ارزش منفرد بر اساس ماتریس‌ها هستند و به طور گسترده در تجزیه‌وتحلیل و فشرده‌سازی داده‌ها استفاده می‌شوند.

در سیستم‌های کنترل، ماتریس‌ها برای مدل‌سازی سیستم‌های دینامیکی مانند سیستم‌های مکانیکی، مدارهای الکتریکی و سیستم‌های کنترل کاربرد دارند. نمایش حالت – فضای یک سیستم پویا مجموعه‌ای از معادلات دیفرانسیل خطی است که تکامل سیستم را در طول زمان توصیف می‌کند و ماتریس‌ها برای نشان‌دادن ضرایب این معادلات به‌خوبی عمل می‌نمایند.

کاربردهای استفاده از ماتریس به زبانی دیگر:

• جبر خطی: ماتریس‌ها به طور گسترده‌ای در جبر خطی، شاخه‌ای از ریاضیات که با معادلات خطی، فضاهای برداری و تبدیل‌های خطی سروکار دارد، استفاده می‌شود. ماتریس‌ها برای نشان‌دادن معادلات خطی و حل سیستم‌های معادلات خطی کاربرد دارند.
• بهینه‌سازی: ماتریس‌ها در مسائل بهینه‌سازی، مانند برنامه‌ریزی خطی، برای نمایش محدودیت‌ها و توابع هدف مسئله استفاده می‌گردند.
• پردازش سیگنال: ماتریس‌ها در پردازش سیگنال برای نمایش سیگنال‌ها و انجام عملیاتی مانند فیلترکردن و تبدیل استفاده می‌شوند.
• تجزیه‌وتحلیل گراف: ماتریس‌ها در تحلیل گراف برای نمایش نمودارها و انجام عملیاتی مانند یافتن کوتاه‌ترین مسیر بین دو گره مفید هستند.
• مکانیک کوانتومی: ماتریس‌ها در مکانیک کوانتومی برای نمایش حالت‌ها و عملیات در سیستم‌های کوانتومی کارایی دارند.

مطلب پیشنهادی: طراحی الگوریتم چیست؟

سخن پایانی

یک آرایه مستطیلی از اعداد، نمادها یا کاراکترها ماتریس نامیده می‌شود. ماتریس‌ها با ترتیب آنها شناسایی می‌شوند. ترتیب ماتریس‌ها به شکل تعدادی ردیف X و تعداد ستون Y داده شده است. یک ماتریس به‌صورت [P] m⨯n نشان داده می‌شود که در آن P ماتریس، m تعداد ردیف‌ها و n تعداد ستون‌ها است. ماتریس‌ها در ریاضیات در حل مسائل متعدد معادلات خطی و بسیاری موارد دیگر مفید هستند. ماتریس‌ها همچنین نقش مهمی در حل معادلات خطی دارند. روش گاوسی و تجزیه LU دو روش مبتنی بر ماتریس برای حل سیستم‌های معادلات خطی هستند و به طور گسترده در مهندسی و علم استفاده می‌شوند. در نتیجه، ماتریس‌ها ابزاری اساسی در ریاضیات می‌باشند و کاربردهای گسترده‌ای در علوم، مهندسی و فناوری دارند. آنها برای نمایش داده‌ها، انجام محاسبات و مدل‌سازی مشکلات دنیای واقعی استفاده می‌گردند.