اتحاد مربع کامل چیست؟

اتحاد مربع کامل چیست؟

در دنیای جبر، اتحاد مربع کامل گویی جادوی ریاضیات را به ارمغان می‌آورد. این ابزار قدرتمند، معادلات پیچیده را به سادگیِ آب خوردن حل می‌کند و درهای تازه‌ای به سوی درک عمیق‌تر مفاهیم ریاضی می‌گشاید. اتحاد مربع کامل هویتی در جبر است که بیان می‌کند مربع مجموع یا تفاضل دو عبارت، برابر با مجموع یا تفاضل مربع آن عبارات به اضافه دو برابر حاصلضرب آن عبارات است. به عبارت دیگر، اگر a و b دو عدد دلخواه باشند، می‌توان نوشت:

(a + b)² = a² + 2ab + b²

(a – b)² = a² – 2ab + b²

تدریس خصوصی ریاضی با بهترین اساتید ایران 😍

کاربردهای اتحاد مربع کامل

اتحاد مربع کامل کاربردهای فراوانی در جبر و فراتر از آن دارد. از جمله این کاربردها می‌توان به موارد زیر اشاره کرد:

• تجزیه و تحلیل معادلات: با استفاده از این فرمول  می‌توان معادلات درجه دوم را به سادگی فاکتورگیری کرد و ریشه‌های آن‌ها را یافت.
• ساده‌سازی عبارات: ابزاری کارآمد برای ساده‌سازی عبارات جبری پیچیده است.
• محاسبات انتگرال: در محاسبات انتگرال، برای حل انتگرال‌های خاص استفاده می‌شود.
• هندسه: در هندسه، برای محاسبه مساحت و محیط اشکال هندسی مانند مربع و مستطیل به کار می‌رود.

مطلب پیشنهادی: چطور ریاضی را برای کنکور بخوانیم؟

اثبات اتحاد مربع کامل

اثبات اتحاد مربع کامل با استفاده از روش‌های مختلفی امکان‌پذیر است. یکی از روش‌های رایج، استفاده از بسط دو جمله‌ای است. به عنوان مثال، برای اثبات فرمول می‌توان به شرح زیر عمل کرد:

(a + b)² = (a + b)(a + b) = a² + ab + ba + b²

با جابجا کردن ab و ba، به فرمول مطلوب می‌رسیم:

(a + b)² = a² + 2ab + b²

اتحاد مربع کامل در معادلات دیفرانسیل: گامی فراتر در دنیای حل معادلات

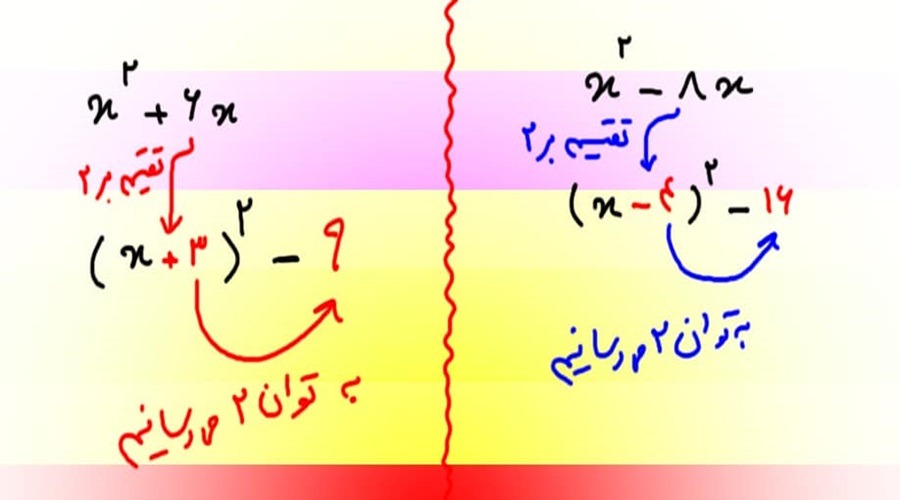
در مورد این اتحاد میتوان گفت ، گویی طلسمی جادویی در دنیای معادلات دیفرانسیل است که دریچه‌ای به سوی روش‌های نوین حل معادلات پیچیده می‌گشاید. در این بخش، به بررسی نقش شگفت‌انگیز این مفهوم در حل معادلات دیفرانسیل می‌پردازیم.

در دنیای معادلات دیفرانسیل، معادلات دیفرانسیل خطی جایگاهی ویژه دارند.  این اتحاد ابزاری کارآمد در حل این نوع معادلات به شمار می‌رود. به عنوان مثال، معادله دیفرانسیل y” + 4y’ + 4y = 0 را با استفاده از اتحاد مربع کامل می‌توان به سادگی حل کرد:

y” + 4y’ + 4y = 0

(y + 2y’)² = 0

y + 2y’ = 0

y(1 + 2y’) = 0

از این معادله، دو حالت y = 0 و 1 + 2y’ = 0 به دست می‌آید که با حل هر کدام، می‌توان جواب‌های معادله دیفرانسیل را یافت. این روش حتی برای افرادی که به دنبال دلایل خاص مانند دلیل یاد نگرفتن ریاضی هستند، مناسب است.

معادلات دیفرانسیل مرتبه بالاتر

کاربرد این اتحاد به  معادلات دیفرانسیل خطی محدود نمی‌شود. در معادلات دیفرانسیل مرتبه بالاتر نیز می‌توان از این مفهوم برای ساده‌سازی معادله و یافتن راه‌حل‌های آن استفاده کرد. به عنوان مثال، معادله دیفرانسیل y”’ + 6y” + 9y’ = 0 را با استفاده از اتحاد مربع کامل می‌توان به معادله دیفرانسیل خطی تبدیل کرد و سپس آن را حل کرد:

y”’ + 6y” + 9y’ = 0

(y’ + 3y”)² = 0

y’ + 3y” = 0

با حل این معادله دیفرانسیل خطی، می‌توان y’ را به دست آورد و سپس با جایگذاری آن در معادله اصلی، y را یافت.

مطلب پیشنهادی: نحوه خواندن ریاضی برای امتحان نهایی

کاربرد اتحاد مربع کامل در تبدیل لاپلاس

این اتحاد در تبدیل لاپلاس نیز نقشی کلیدی ایفا می‌کند. با استفاده از این مفهوم، می‌توان انتگرال لاپلاس توابع مختلف را به سادگی محاسبه کرد. به عنوان مثال، انتگرال لاپلاس تابع f(t) = t² را با استفاده از اتحاد مربع کامل می‌توان به صورت زیر محاسبه کرد:

L{t²} = ∫₀^∞ t²e^(-st) dt

= ∫₀^∞ (t + 0)²e^(-st) dt

= ∫₀^∞ (t² + 0t + 0t² + 0²)e^(-st) dt

= ∫₀^∞ (t² + 2t + 1)e^(-st) dt – ∫₀^∞ e^(-st) dt

با ادامه محاسبه و استفاده از خواص تبدیل لاپلاس، می‌توان انتگرال لاپلاس تابع f(t) = t² را به دست آورد

مطلب پیشنهادی: روش های تندخوانی برای کنکور

اتحاد مربع کامل در دنیای برنامه‌نویسی: الگوریتم‌ها و کاربردها

این اتحاد ، در آموزش برنامه‌نویسی، دریچه‌ای به سوی الگوریتم‌های کارآمد و کاربردهای نوین می‌گشاید. در این بخش، به بررسی نقش شگفت‌انگیز این مفهوم در برنامه‌نویسی و معرفی الگوریتم‌های مرتبط با آن می‌پردازیم.

الگوریتم فاکتورگیری:

یکی از کاربردهای اساسی در برنامه‌نویسی، فاکتورگیری عبارات جبری است. به عنوان مثال، الگوریتم زیر برای فاکتورگیری عبارات درجه دوم با استفاده از اتحاد مربع کامل ارائه می‌شود:

این الگوریتم ضرایب a، b و c عبارت درجه دوم را به عنوان ورودی دریافت می‌کند و دو عبارت خطی که حاصل فاکتورگیری عبارت درجه دوم هستند را به عنوان خروجی برمی‌گرداند.

الگوریتم ساده‌سازی عبارات:

اتحاد مربع کامل در ساده‌سازی عبارات جبری نیز نقشی کلیدی ایفا می‌کند. الگوریتم‌های مختلفی برای ساده‌سازی عبارات جبری وجود دارند. به عنوان مثال، الگوریتم زیر برای ساده‌سازی عبارات درجه دوم با استفاده از اتحاد مربع کامل ارائه می‌شود: این الگوریتم ضرایب a، b و c عبارت درجه دوم را به عنوان ورودی دریافت می‌کند و عبارت ساده‌شده را به عنوان خروجی برمی‌گرداند.

مطلب پیشنهادی: روش های تست زنی برای کنکور

کاربردهای اتحاد مربع کامل در هوش مصنوعی

اتحاد مربع کامل در حوزه آموزش هوش مصنوعی نیز کاربردهای مختلفی دارد. به عنوان مثال، از این مفهوم در الگوریتم‌های یادگیری ماشین برای ساده‌سازی مدل‌ها و افزایش دقت آنها استفاده می‌شود. همچنین، در رباتیک برای کنترل حرکت ربات‌ها و بهینه‌سازی مسیر آنها استفاده می‌شود.

مطلب پیشنهادی: نحوه خواندن فلسفه برای کنکور

اتحاد مربع کامل: کلیدی جادویی در دنیای مهندسی و علوم کاربردی

این نوع اتحاد کلیدی جادویی  در دنیای مهندسی و علوم کاربردی است که دریچه‌ای به سوی حل مسائل پیچیده و بهینه‌سازی فرایندها می‌گشاید. در این بخش، به بررسی نقش شگفت‌انگیز این مفهوم در حوزه‌های مختلف مهندسی و علوم کاربردی می‌پردازیم.

مهندسی برق:

در مهندسی برق، برای تحلیل مدارهای الکتریکی، محاسبه امپدانس و طراحی فیلترها استفاده می‌شود. به عنوان مثال، در تحلیل مدارهای RLC، برای حل معادلات دیفرانسیل و تعیین پاسخ مدار به سیگنال‌های ورودی استفاده می‌شود.

مهندسی مکانیک:

در مهندسی مکانیک، برای تحلیل حرکت اجسام، محاسبه تنش و کرنش و طراحی سازه‌ها استفاده می‌شود. به عنوان مثال، در تحلیل حرکت یک جسم در میدان گرانشی، برای محاسبه معادله حرکت و تعیین موقعیت و سرعت جسم در طول زمان استفاده می‌شود.

مهندسی عمران:

در مهندسی عمران، برای تحلیل سازه‌ها، طراحی پل‌ها و ساختمان‌ها و بهینه‌سازی مصرف مصالح استفاده می‌شود. به عنوان مثال، در تحلیل تنش در تیرهای خمیده، برای محاسبه توزیع تنش در طول تیر و تعیین حداکثر تنش مجاز استفاده می‌شود.

علوم کامپیوتر:

در علوم کامپیوتر،  در الگوریتم‌های مختلف، بهینه‌سازی کد و فشرده‌سازی داده‌ها استفاده می‌شود. به عنوان مثال، در الگوریتم‌های مرتب‌سازی، برای ساده‌سازی محاسبات و افزایش سرعت مرتب‌سازی استفاده می‌شود.

شیمی:

در شیمی، برای محاسبه ترمودینامیکی، شبیه‌سازی ساختار مولکول‌ها و طراحی کاتالیزورها استفاده می‌شود. به عنوان مثال، در محاسبه انرژی آزاد گیبس یک واکنش شیمیایی، برای ساده‌سازی معادلات و تعیین تعادل واکنش استفاده می‌شود.

مطلب پیشنهادی: بهترین شغل‌های رشته انسانی برای خانم ها

مقایسه اتحاد مربع کامل و اتحاد مکعب کامل

در دنیای جبر، اتحادها حکم یارانی وفادار را دارند که به حل معادلات و ساده‌سازی عبارات پیچیده یاری می‌رسانند. در این میان، اتحاد مربع کامل و اتحاد مکعب کامل دو یار قدرتمند هستند که در زمینه توان‌ها به ما کمک می‌کنند. در این بخش، به سفری در دنیای توان‌ها می‌رویم و هر دو اتحاد باهم  مقایسه می‌کنیم.

شباهت‌ها:

• هر دو اتحاد هویتی هستند: اتحاد مربع کامل هویتی است که برابری دو عبارت را با بسط مربع مجموع یا تفاضل دو عبارت بیان می‌کند. اتحاد مکعب کامل نیز هویتی است که برابری دو عبارت را با بسط مکعب مجموع یا تفاضل دو عبارت بیان می‌کند.
• کاربرد در فاکتورگیری: از هر دو اتحاد می‌توان برای فاکتورگیری عبارات جبری استفاده کرد. اتحاد مربع کامل برای فاکتورگیری عبارات درجه دوم و اتحاد مکعب کامل برای فاکتورگیری عبارات درجه سوم به کار می‌رود.
• کاربرد در ساده‌سازی عبارات: از هر دو اتحاد می‌توان برای ساده‌سازی عبارات جبری استفاده کرد.

تفاوت‌ها:

• نوع توان: اتحاد مربع کامل بر پایه توان دوم و اتحاد مکعب کامل بر پایه توان سوم بنا شده است.
• پیچیدگی: اتحاد مربع کامل از نظر مفهومی و اثباتی ساده‌تر از اتحاد مکعب کامل است.
• کاربرد: اتحاد مربع کامل کاربرد گسترده‌تری در جبر و فراتر از آن دارد، در حالی که اتحاد مکعب کامل عمدتاً در فاکتورگیری عبارات درجه سوم و ساده‌سازی عبارات مربوط به توان سوم استفاده می‌شود.

نتیجه گیری

در این مقاله، سفری در گذر زمان و دنیای ریاضیات و کاربردهای آن داشتیم و اتحاد مربع کامل را از زوایای مختلف مورد بررسی قرار دادیم. این اتحاد ، گویی گوهری گرانبها در دنیای جبر، ریاضیات، مهندسی و علوم کاربردی است که دریچه‌ای به سوی مفاهیم عمیق‌تر، روش‌های نوین حل معادلات، ساده‌سازی عبارات پیچیده و در نهایت، درک بهتر دنیای پیرامونمان می‌گشاید. در این مقاله آموختیم که اتحاد مربع کامل ریشه در اعماق تاریخ دارد و از گذشته تا کنون توسط ریاضی‌دانان برجسته مورد مطالعه و توسعه قرار گرفته است. همچنین، کاربردهای این مفهوم در معادلات دیفرانسیل، برنامه‌نویسی، مهندسی و علوم مختلف نشان می‌دهد که اتحاد مربع کامل، ابزاری کارآمد و فراگیر در حل مسائل گوناگون است.

در نهایت، با مقایسه این اتحاد با دیگر اتحادها و همچنین اتحاد مکعب کامل، جایگاه منحصر به فرد و اهمیت این مفهوم را در دنیای ریاضیات و کاربردهای آن به طور کامل درک کردیم.