الگوریتم فیبوناچی چیست؟

الگوریتم فیبوناچی، یکی از بنیادی‌ترین و پرکاربردترین الگوریتم‌ها در علوم کامپیوتر و ریاضیات است. این طراحی الگوریتم بر اساس دنباله‌ای از اعداد شناخته می‌شود که در آن هر عدد برابر با مجموع دو عدد قبلی است. این دنباله به نام ریاضیدان ایتالیایی، لئوناردو فیبوناچی، نامگذاری شده است. اگرچه این الگوریتم به سادگی بیان می‌شود، اما کاربردهای گسترده‌ای در حوزه‌های مختلف از جمله علوم کامپیوتر، آموزش ریاضی، اقتصاد و حتی طبیعت دارد. در این مقاله، به بررسی جامع الگوریتم فیبوناچی، کاربردهای آن و پیاده‌سازی‌های مختلف آن خواهیم پرداخت.

آموزش برنامه نویسی پایتون در هر لحظه و هر جا با کارآموز

دنباله فیبوناچی

دنباله فیبوناچی یک دنباله عددی است که از عدد ۰ و ۱ شروع می‌شود و هر عدد بعدی با جمع دو عدد قبلی به دست می‌آید. به عبارت دیگر، اگر F(n) نشان‌دهنده nامین عدد فیبوناچی باشد، آن‌گاه داریم:

F(0) = 0

F(1) = 1

F(n) = F(n-1) + F(n-2) برای n ≥ 2

چند جمله اول از دنباله فیبوناچی به صورت زیر است:

0, 1, 1, 2, 3, 5, 8, 13, 21, …

مطلب پیشنهادی: صف در ساختمان داده چیست؟

الگوریتم محاسبه دنباله فیبوناچی

ساده‌ترین روش برای محاسبه nامین عدد فیبوناچی، استفاده از تعریف بازگشتی آن است. در این روش، برای محاسبه هر عدد، باید دو عدد قبلی را محاسبه کنیم. اما این روش از نظر محاسباتی بسیار پرهزینه است، زیرا برای محاسبه هر عدد، بسیاری از محاسبات تکراری انجام می‌شود.

روش کارآمدتر برای محاسبه دنباله فیبوناچی، استفاده از یک حلقه تکرار است. در این روش، مقادیر دو عدد قبلی را در دو متغیر ذخیره می‌کنیم و در هر تکرار، مقدار عدد بعدی را محاسبه کرده و مقادیر متغیرها را به‌روزرسانی می‌کنیم.

مطلب پیشنهادی: پردازش داده چیست؟

پیاده‌سازی الگوریتم فیبوناچی

الگوریتم فیبوناچی را می‌توان در زبان‌های برنامه‌نویسی مختلفی پیاده‌سازی کرد. در زیر، مثالی از پیاده‌سازی این الگوریتم به زبان پایتون ارائه شده است:

کاربردهای الگوریتم فیبوناچی

الگوریتم فیبوناچی کاربردهای بسیار گسترده‌ای در حوزه‌های مختلف دارد، از جمله:

• علوم کامپیوتر: الگوریتم فیبوناچی در طراحی الگوریتم‌های جستجو، مرتب‌سازی، و تقسیم و غلبه استفاده می‌شود.
• ریاضیات: دنباله فیبوناچی در بسیاری از مسائل ریاضی مانند نظریه اعداد، ترکیبیات و هندسه ظاهر می‌شود.
• اقتصاد: از دنباله فیبوناچی برای مدل‌سازی پدیده‌های اقتصادی مانند رشد جمعیت و قیمت سهام استفاده می‌شود.
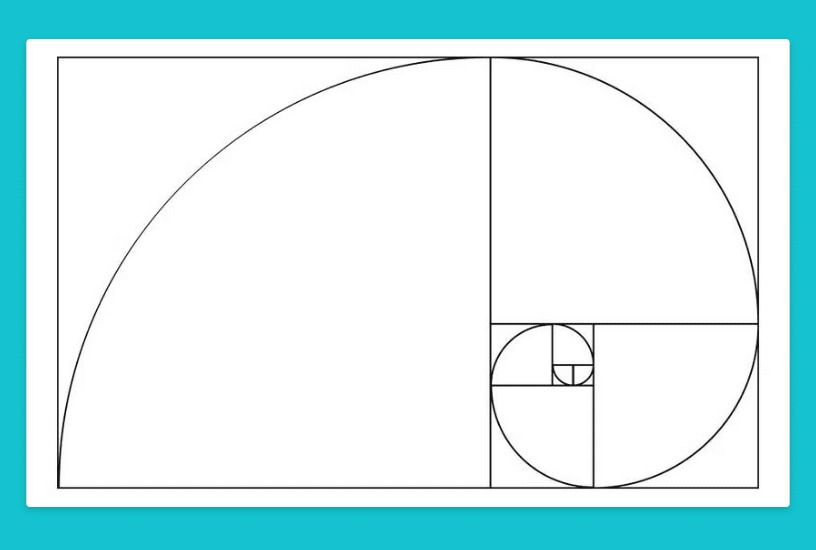
• طبیعت: نسبت طلایی، که در بسیاری از پدیده‌های طبیعی مانند گلبرگ‌های گل، صدف‌ها و مارپیچ‌های کهکشان‌ها دیده می‌شود، با دنباله فیبوناچی ارتباط نزدیکی دارد.
• هنر و معماری: بسیاری از هنرمندان و معماران از نسبت طلایی و دنباله فیبوناچی برای ایجاد آثار هنری زیبا و متعادل استفاده می‌کنند.

بهبود عملکرد الگوریتم فیبوناچی

برای بهبود عملکرد الگوریتم فیبوناچی، می‌توان از روش‌های مختلفی استفاده کرد، از جمله:

• حافظه‌سازی: در روش حافظه‌سازی، نتایج محاسبات قبلی را ذخیره می‌کنیم تا از محاسبات تکراری جلوگیری کنیم.
• روش ماتریسی: با استفاده از روش‌های ماتریسی، می‌توان nامین عدد فیبوناچی را در زمان لگاریتمی محاسبه کرد.

مطلب پیشنهادی: قانون اهم چیست؟

کاربردهای پیشرفته الگوریتم فیبوناچی

الگوریتم فیبوناچی، فراتر از محاسبه ساده اعداد در یک دنباله، در بسیاری از مسائل پیچیده و پیشرفته کاربرد دارد. این الگوریتم، با ساختار ریاضی منحصربه‌فرد خود، به عنوان ابزاری قدرتمند در حل مسائل مختلف در حوزه‌های گوناگون عمل می‌کند. در این بخش، به برخی از کاربردهای پیشرفته الگوریتم فیبوناچی خواهیم پرداخت.

1. علوم کامپیوتر و الگوریتم‌های پیچیده‌تر

• جستجوی دودویی فیبوناچی: این الگوریتم جستجو، با استفاده از نسبت طلایی فیبوناچی، بهینه‌تر از جستجوی دودویی سنتی عمل می‌کند.
• مرتبه‌سازی فیبوناچی: برخی الگوریتم‌های مرتب‌سازی، از خواص دنباله فیبوناچی برای تقسیم داده‌ها و مرتب‌سازی آن‌ها استفاده می‌کنند.
• ساختارهای داده: درخت‌های فیبوناچی، نوعی از درخت‌های جستجوی دودویی هستند که از خواص اعداد فیبوناچی برای انجام عملیات مختلف مانند درج، حذف و جستجو استفاده می‌کنند.
• برنامه‌نویسی پویا: بسیاری از مسائل در آموزش برنامه‌نویسی پویا، با استفاده از روابط بازگشتی مشابه دنباله فیبوناچی، حل می‌شوند.

2. ریاضیات و علوم پایه

• نظریه اعداد: دنباله فیبوناچی در اثبات بسیاری از قضایای نظریه اعداد و مطالعه خواص اعداد صحیح کاربرد دارد.
• ترکیبیات: در مسائل شمارش و ترکیبیات، دنباله فیبوناچی به عنوان یک ابزار قدرتمند برای حل مسائل مختلف استفاده می‌شود.
• هندسه: نسبت طلایی، که با دنباله فیبوناچی ارتباط نزدیکی دارد، در هندسه فراکتال و مطالعه اشکال هندسی پیچیده کاربرد دارد.

3. اقتصاد و مالی

• مدل‌سازی بازارهای مالی: از دنباله فیبوناچی برای پیش‌بینی روند بازارهای مالی و تعیین سطوح حمایت و مقاومت استفاده می‌شود.
• مدیریت ریسک: در مدیریت ریسک مالی، از نسبت طلایی و اعداد فیبوناچی برای تعیین اندازه موقعیت‌های معاملاتی استفاده می‌شود.

4. علوم طبیعی

• بیولوژی: بسیاری از پدیده‌های طبیعی مانند رشد گیاهان، ساختار صدف‌ها و مارپیچ‌های کهکشان‌ها، با نسبت طلایی و دنباله فیبوناچی مرتبط هستند.
• فیزیک: در برخی از مسائل فیزیک، از جمله فیزیک ذرات و مکانیک کوانتومی، از دنباله فیبوناچی استفاده می‌شود.

5. هنر و معماری

• طراحی هنری: نسبت طلایی و دنباله فیبوناچی در طراحی آثار هنری، از جمله نقاشی، مجسمه‌سازی و معماری، برای ایجاد تعادل و زیبایی استفاده می‌شود.
• موسیقی: در موسیقی، از نسبت طلایی و دنباله فیبوناچی برای ساخت ملودی‌ها و آهنگسازی استفاده می‌شود.

6. هوش مصنوعی

• یادگیری ماشین: الگوریتم‌های یادگیری ماشین مبتنی بر شبکه‌های عصبی، از ساختارهای الهام گرفته از طبیعت، مانند شبکه‌های عصبی مصنوعی با الهام از مغز انسان، استفاده می‌کنند. این شبکه‌ها می‌توانند از الگوهای مشابه دنباله فیبوناچی برای یادگیری و پیش‌بینی استفاده کنند.
• پردازش تصویر: الگوریتم‌های پردازش تصویر، مانند فیلترهای تصویری مبتنی بر فیبوناچی، برای بهبود کیفیت تصاویر استفاده می‌شوند.

مطلب پیشنهادی: بهترین ابزارهای ساخت عکس با هوش مصنوعی

رابطه بین الگوریتم فیبوناچی و نسبت طلایی

یکی از جذاب‌ترین جنبه‌های دنباله فیبوناچی، ارتباط عمیق آن با نسبت طلایی است. این نسبت، که با نماد φ (فی) نشان داده می‌شود، یک عدد اصم است که تقریباً برابر با 1.618 است. نسبت طلایی در طبیعت، هنر، آموزش معماری و بسیاری از حوزه‌های دیگر به وفور یافت می‌شود و به عنوان نمادی از زیبایی و تعادل در نظر گرفته می‌شود.

ارتباط ریاضی

اگر به نسبت دو عدد متوالی در دنباله فیبوناچی توجه کنیم، متوجه می‌شویم که با افزایش اندیس این اعداد، نسبت آن‌ها به عدد طلایی نزدیک‌تر می‌شود. به عبارت دیگر:

lim (F(n+1) / F(n)) = φ

n→∞

این بدان معناست که هر چه جلوتر در دنباله فیبوناچی برویم، نسبت هر عدد به عدد قبلی خود به عدد طلایی نزدیک‌تر خواهد شد. این رابطه ریاضی، ارتباط عمیقی بین دنباله فیبوناچی و نسبت طلایی برقرار می‌کند.

نسبت طلایی در طبیعت

• گیاهان: تعداد گلبرگ‌های بسیاری از گل‌ها، تعداد مارپیچ‌های دانه‌های آفتابگردان و آرایش برگ‌ها روی ساقه گیاهان، اغلب با اعداد فیبوناچی و نسبت طلایی مرتبط هستند.
• حیوانات: نسبت‌های مختلف بدن بسیاری از حیوانات، مانند نسبت طول بدن به طول دم یا نسبت طول بال به طول بدن پرندگان، به نسبت طلایی نزدیک است.
• انسان: نسبت‌های مختلف بدن انسان، مانند نسبت طول سر به طول بدن یا نسبت طول دست به طول ساعد، نیز با نسبت طلایی مرتبط هستند.

نسبت طلایی در هنر و معماری

• نقاشی: بسیاری از نقاشان بزرگ از نسبت طلایی در آثار خود استفاده کرده‌اند تا تعادل و زیبایی بصری را ایجاد کنند.
• معماری: از اهرام مصر گرفته تا ساختمان‌های مدرن، بسیاری از بناهای تاریخی از نسبت طلایی برای ایجاد تناسب و زیبایی استفاده کرده‌اند.

کاربردهای نسبت طلایی در علوم کامپیوتر

• گرافیک کامپیوتری: نسبت طلایی در طراحی رابط‌های کاربری، ایجاد انیمیشن‌ها و طراحی بازی‌های رایانه‌ای برای ایجاد تعادل بصری استفاده می‌شود.
• فشرده‌سازی داده: برخی از الگوریتم‌های فشرده‌سازی داده، از خواص نسبت طلایی برای بهبود کارایی استفاده می‌کنند.

دلایل اهمیت ارتباط فیبوناچی

• زیبایی شناسی: نسبت طلایی به عنوان یک استاندارد زیبایی شناختی در نظر گرفته می‌شود و در بسیاری از زمینه‌ها برای ایجاد تعادل و هماهنگی استفاده می‌شود.
• سادگی و پیچیدگی: دنباله فیبوناچی به عنوان یک ساختار ریاضی ساده، قادر است پدیده‌های پیچیده طبیعی و هنری را توضیح دهد.
• کاربردهای عملی: درک ارتباط بین دنباله فیبوناچی و نسبت طلایی، به ما امکان می‌دهد تا از این مفاهیم در حل مسائل مختلف در علوم کامپیوتر، ریاضیات، هنر و سایر حوزه‌ها استفاده کنیم.

در نهایت، رابطه بین الگوریتم فیبوناچی و نسبت طلایی، یکی از شگفت‌انگیزترین پدیده‌های ریاضی است که نشان می‌دهد چگونه یک ساختار ریاضی ساده می‌تواند در توصیف پیچیدگی‌های جهان طبیعی و مصنوعی به ما کمک کند.

نتیجه‌گیری

در این پژوهش، به بررسی عمیق الگوریتم فیبوناچی و ارتباط شگفت‌انگیز آن با نسبت طلایی پرداختیم. از تعریف ساده دنباله فیبوناچی آغاز کرده و به کاربردهای گسترده آن در حوزه‌های مختلف از جمله علوم کامپیوتر، ریاضیات، اقتصاد، هنر و طبیعت پرداختیم. مشاهده کردیم که نسبت طلایی، به عنوان یک عدد ثابت و فراگیر در طبیعت، با دنباله فیبوناچی ارتباط تنگاتنگی دارد و در بسیاری از پدیده‌های طبیعی و مصنوعی به چشم می‌خورد. این ارتباط عمیق بین ریاضیات، طبیعت و زیبایی، نشان می‌دهد که الگوریتم فیبوناچی و نسبت طلایی، نه تنها مفاهیم ریاضی هستند، بلکه کلید درک بسیاری از پدیده‌های اطراف ما هستند. در طول این پژوهش، به این نتیجه رسیدیم که الگوریتم فیبوناچی، فراتر از یک الگوریتم محاسباتی ساده، یک ابزار قدرتمند برای مدل‌سازی، تحلیل و درک پدیده‌های پیچیده است. با توجه به کاربردهای گسترده الگوریتم فیبوناچی و نسبت طلایی، می‌توان نتیجه گرفت که مطالعه و بررسی بیشتر این مفاهیم، می‌تواند به پیشرفت‌های چشمگیری در حوزه‌های مختلف علم و فناوری منجر شود. همچنین، درک عمیق از این مفاهیم، به ما کمک می‌کند تا زیبایی و نظم نهفته در طبیعت را بهتر درک کنیم.

در نهایت، می‌توان گفت که الگوریتم فیبوناچی و نسبت طلایی، دو مفهوم به ظاهر ساده، اما با عمق و پیچیدگی بسیار زیاد هستند که همچنان موضوع پژوهش‌های بسیاری از دانشمندان و محققان هستند. با پیشرفت تکنولوژی و روش‌های محاسباتی، می‌توان انتظار داشت که در آینده کاربردهای جدید و شگفت‌انگیزی برای این مفاهیم کشف شود.